vol. 15 no. 1, March, 2010
vol. 15 no. 1, March, 2010 | ||||
Search engine marketing is a method of Internet marketing that increases the visibility of a company's Website in search engine listings. In this marketing method, the business opportunity of paid search advertising is growing fast. According to existing historical evidence, the growing scale of this marketing method is very fast compared to traditional advertising or other online marketing methods (Elliott 2006). In North American, the total market size of this marketing method was about US$12.2 billion in 2007, and it grew by 30% in 2006. Moreover, and even more significant, this marketing method spending is now projected to grow to US$25.2 billion in 2011 (Sherman 2008).
Search engine marketing can be divided into two broad areas: search engine optimization and pay-per-click (Sherman 2008).
Search engine optimization is the process of developing, customizing or retooling a Web page so that it achieves a sustained high-ranking on search engine listings. According to the literature (see, for example, Spink et al. 2001), the majority of users (85.2%) view only the first page of the listings. Thus, if the entry page of a Website can be placed into the top rankings by a suitable optimisation process, then it can achieve a best advertising effect. However, it is a hard task to place a Web page into the top rankings unless the quality of the page content is superior to others.
Pay-per-click is another technique, whereby the advertisers typically bid on the advertisers' keyword list relevant to their target market. When the user's query matches the list, the advertiser's destination URL may be shown to the user. These links are called sponsored links or sponsored advertisements, and appear adjacent to or above the normal results. The search engine owners place the advertiser's destination URL into the top position of sponsored links for the advertiser who bids on the highest price and the bidding process may result in higher bidding price for popular keywords.
Alternatively, the advertisers also can focus on relatively low-cost keywords or phrases, called suggested keywords, which are relevant to the popular keywords, by a keyword suggestion process. On the one hand, the advertisers can adequately bid on a large number of suggested keywords to minimize their total cost, although the advertising effect of these keywords may be lower than the popular keywords. On the other hand, the search engine owners must provide an appropriate tool to attract more advertisers to buy advertisements to maximize their total revenue. Thus, using a suitable keyword suggestion process to generate a list of target keywords is an important issue for advertisers and search engine owners. In this paper, we focus on to propose a new keyword suggestion process to the search engine owners. When this process is built from the search engine owners, the advertisers can bid on the suggested keywords generated from this process. If the suggested keywords are highly related to the popular keywords, the search engine owners should attract more advertisers to increase their advertising budget.
Although many pay-per=click search providers exist in the current Internet, Yahoo Search Marketing (Yahoo 2006), Google AdWords (Google 2006), and Microsoft adCenter (Microsoft 2006) were the largest in 2007 (Sherman 2008).
Yahoo (formerly Overture, formerly Goto.com) was first to propose the concept of pay-per-click. Previously, the search engines had extracted the description values of the meta tags in HTML to obtain the description of the page content. Obviously, some webmasters may try to improve the ranking of their Website by a manual process to manipulate the content of the meta tags. Goto.com focused on roughly the top 1,000 most popular keywords, employing experts and consultants to create hand-crafted pages (Jansen and Mullen 2008) to overcome this problem. When Goto.com introduced the concept of sponsored search, each page was associated with a suggested keyword list. The suggested keyword list was open to bids and the advertisers could request to add the advertiser's keyword list into a suitable suggested keyword list by a bidding process. In other words, Goto.com could ensure that the advertising content was relevant to the suggested keyword list. Given the rapid growth of sponsored search, the bidding process is now partially automated (Mordkovich and Mordkovich 2007).
Google proposed an AdWords service in 2000 and it became Google's main source of revenue (2008). The main characteristic of AdWords is the charging model of sponsored links, which uses the click through rate and cost per click to charge a suitable price for advertisers (Lves 2005). The advertisers can control the amount of budget and time they wish to spend on advertising.
Microsoft was the last of the three big search engines (Google, Yahoo and MSN Live Search, now Bing) to develop its own pay-per-click service. Previously, the advertising of Microsoft was provided by Overture. Microsoft decided to launch its own adCenter service in 2006 when search engine marketing is growing fast. In adCenter, the position of sponsored links is decided by the advertisers' budget and is similar to Google AdWords. The main difference between adCenter and AdWords is that the former is integrated with MSN's member database, that is, the advertisers can decide the position of sponsored links according to sex, age, and place of residence by tracking the member database.
The existing providers fail to consider the semantic relationships between the user's query and the suggested keywords. That is, the relevant suggested keywords, not containing the input query, are often ignored to suggest.
This paper proposes a novel keyword suggestion system, called LIK, to suggest relevant and important keywords, and to measure the degree of similarity between the user's query and each relevant keyword. This system contains the following two stages: training and suggestion. In the training stage, it updates the training parameter based on the methods of latent semantic analysis (Deerwester et al. 1990) and probabilistic latent semantic analysis (Hofmann 1999). In the suggestion stage, it first applies breadth-first search and the concept of inverse link to build a semantic graph. Then, it transforms the training parameter into the edge weight of the graph. Finally, the relevant keywords with the degree of similarity are suggested to the user for viewing or accessing according to the edge weight of the graph. In summary, the bases of latent semantic analysis, probabilistic latent semantic analysis and the semantic graph are all based on the semantic analysis between the query terms and the Web pages.
We make the following salient contributions in this paper. We propose a system that is based on several semantic analysis methods. We define a new performance metric, DIST, to compare the experimental results of different systems to fairly evaluate the performance of different systems. Moreover, this metric also can be applied to evaluate other information retrieval problems, such as document clustering and content matching. We design several mechanisms to achieve highly cost effective and noticeable improvements.
The rest of this paper is organized as follows. Next, previous research is reviewd; the following section presents the system's architecture, after which the performance comparisons between our system and other systems are shown, along with the simulation results for various parameters and the final section concludes the paper and discusses future directions.
In this section, we discuss two related literatures: keyword suggestion and termination criteria for probabilistic latent semantic analysis.
Keyword suggestion is a relatively new and rapidly expanding research field, whose main goal is to generate a list of suggested keywords. Many systems are available on the Internet and currently available systems are shown in Table 1. CatS (Radovanovic and Ivanovic 2006) used a separate category tree that derived from the dmoz taxonomy to arrange all suggested keywords. Highlight (Wu and Chen 2003) adopted a lexical analysis and a probabilistic analysis to construct a concept hierarchy for all relevant keywords. Credo (Carpineto and Romano 2004) applied a formal concept analysis to construct all suggested keywords in a hierarchy form that allows users to query Web pages and judges the relevant results. Carrot2 (Osinski and Weiss 2005) used the sentences with variable length words as the candidate keywords, then, it utilized a suffix tree clustering to identify which one should be suggested. Google Proximity Search (Ranks.NL 2008) used several search engines to collect the relevant Web pages in response to the seed keyword, then, it expanded new suggested keywords in its proximity range. Google AdWords (Google 2006) and Yahoo Search Marketing (Yahoo 2006) analysed the content of the query log file to suggest the relevant keywords. Clusty (Segev et al. 2007) adopted the concept of concise all-pairs profiling to match all possible pairs of relevant keywords. WordTracker (2008) produced a list of suggested keywords by using the concept of query expansion.
| System | Access URL |
| CatS | http://stribog.im.ns.ac.yu/cats/servlet/CatS?searchEngine=AltaVista |
| Highlight | http://Highlight.njit.edu/ |
| Credo | http://Credo.fub.it/ |
| Carrot2 | http://search.Carrot2.org/ |
| Google Proximity Search | http://www.rapidkeyword.com/ |
| Google AdWords | https://adwords.google.com/ |
| Yahoo Search Marketing | https://signup13.marketingsolutions.yahoo.com/ |
| Clusty | http://Clusty.com/ |
| WordTracker | http://freekeywords.wordtracker.com/ |
| LIK | http://cayley.sytes.net/LIK_english |
A classical method to represent the co-occurrences of terms and documents is term matching. However, this method exists two problems: synonymy and polysemy. Deerwester et al. (1990) proposed a latent semantic analysis model to address the problem of synonymy. Latent semantic analysis uses the singular value decomposition, a mathematical technique that reduces the dimension of the matrix, to capture lexical similarities between terms and documents. However, it fails to deal with the problem of polysemy since a single vector in the result of singular value decomposition represents only one term (Ishida and Ohta 2002). Another drawback of latent semantic analysis is that it lacks a solid statistical foundation and, hence, is more difficult to use by combining it with other models (Hofmann 1999).
To overcome these drawbacks, Hofmann (1999) proposed a probabilistic method, called probabilistic latent semantic analysis, to discover a latent semantic space from terms and documents. It is more flexible and has a more solid statistical foundation than standard latent semantic analysis. Additionally, probabilistic latent semantic analysis can deal with the problem of polysemy and can explicitly distinguish between different meanings and different types of term usage. Probabilistic latent semantic analysis uses an aspect model to identify the hidden semantic relationships among terms and documents. In the aspect model, the terms and documents are considered as independent of each other.
Probabilistic latent semantic analysis uses an expectation maximization algorithm for maximum likelihood estimation; it also guarantees a convergent behaviour for the iterative procedure. The target of probabilistic latent semantic analysis is to maximize the log-likelihood function by using the expectation maximization algorithm. Probabilistic latent semantic analysis defines that a local optimal solution is reached if the improvement value of the log-likelihood function between two consecutive iterations is less than a predefined threshold.
Although probabilistic latent semantic analysis can converge to the local optimal solution, it may take a long time to reach this solution. To achieve faster response time for expectation maximization algorithm, many researchers used the following two termination criteria to decide whether the algorithm should stop or whether the processing should proceed: (1) setting a fixed number of iterations to stop the algorithm or (2) using a more relaxed threshold to determine whether the algorithm should terminate.
Some researchers (Gibson et al. 2005; Metaxoglou and Smith 2007; Nguyen et al. 2007) used a fixed number of iterations to stop the algorithm to save execution time when it cannot to reach the local optimal solution within the range of iterations.
Other researchers used a more relaxed threshold to determine whether the algorithm should terminate. Ristad and Yianilos (1998) terminated the algorithm when the increased total probability of training corpus among consecutive iterations falls below a fixed threshold rate. Markatou (2000) calculated the weighted likelihood estimates on the bootstrap sub-samples that were drawn from whole data set by the method of moment estimates for each iteration. The algorithm should be terminated if the estimate values are less than or equal to a predefined quantile value. Zhang and Goldman (2001) first selected a set of unlabelled data in the expectation step, then they calculated a diverse density probability from all selected data in the maximization step. The algorithm should be terminated if the probability is less than or equal to a predefined probability value. Petersen and Winther (2005) applied a negative log-likelihood function as the cost function of the algorithm. Please revise the sentence as follows: The termination criterion is defined as the difference in cost function values of two successive iterations less than the threshold value.
The expectation maximization algorithm uses a fixed number of iterations or a relaxed threshold as the termination criterion has the following two main problems. First, if it takes a small number of iterations or a larger threshold value, it may result in the difference being large compared with the final solution and the local optimal solution. Secondly, if it takes a large number of iterations or a small threshold value, it may result in the number of iterations becoming very large when the improvement value is very small when the solution is close to the local optimal solution.
To solve theses problems, we decided to combine the concept of the improvement value and improvement progress history as the termination criterion. Since the improvement value and improvement progress history are not always equal for each iteration, the number of iterations required to run varies. That is, the combined technique can ensure that the number of iterations is dynamically determined. In summary, we focus on applying this technique to find a cost effective solution within a controlled period of time rather than to find the local optimal solution.
In this section, we propose an integrated keyword suggestion system, called LIK, as shown in Figure 1. The system involves the following two stages: training and suggestion, which are described below.
The main objective of this stage is to generate the training parameter, called the query-by-document matrix, which is the main source of the suggestion stage, based on the methods of latent semantic analysis and probabilistic latent semantic analysis.
First, the training stage uses the AOL Query Log (AOL 2006) as terms and all collected Web pages as documents to form a vector-space-model matrix. The query log consists of about twenty million search query terms collected from about 650,000 users. Then, this stage transforms the vector-space-model matrix into the query-by-document matrix using the latent semantic analysis and intelligent probabilistic latent semantic analysis modules.
The core module of this stage is intelligent probabilistic latent semantic analysis, which is extended from the probabilistic latent semantic analysis method, and which improves the termination criteria of probabilistic latent semantic analysis. Compared to probabilistic latent semantic analysis, the termination criteria of our proposed method have two mechanisms: one based on the local optimal solution, the other based on the improvement value at each iteration and the improvement progress history. The benefit of the second criterion is that it can prevent a relatively small improvement in performance when the solution is close to the local optimal solution. Thus, intelligent probabilistic latent semantic analysis can skilfully reduce the number of iterations required to run this stage and this property should be able to form the query-by-document matrix relatively quickly. In short, the purpose of intelligent probabilistic latent semantic analysis is intended to yield a cost effective solution within a controlled period of time rather than to reach the local optimal solution.
The probabilistic latent semantic analysis method computes the relevant probability distributions by selecting the model parameters that maximize the probability of the observed data, i.e., the likelihood function. The standard method for maximum likelihood estimation is the expectation maximization algorithm. For a given initialization, the likelihood function increases with each iteration of the expectation maximization algorithm until the local optimal solution is reached, so that the quality of solution can be highly variable depends on the initialization values. In this stage, we use the parameters of the latent semantic analysis probability model as the initial parameters in the latent semantic analysis module. Rather than trying to predict the best initial parameters from a set of data, this probability model focuses on how to find a good way to initialize.
Repeatedly, the training stage consecutively executes the modules of latent semantic analysis and intelligent probabilistic latent semantic analysis in background to form a new query-by-document matrix. The detailed descriptions of these two modules follow..
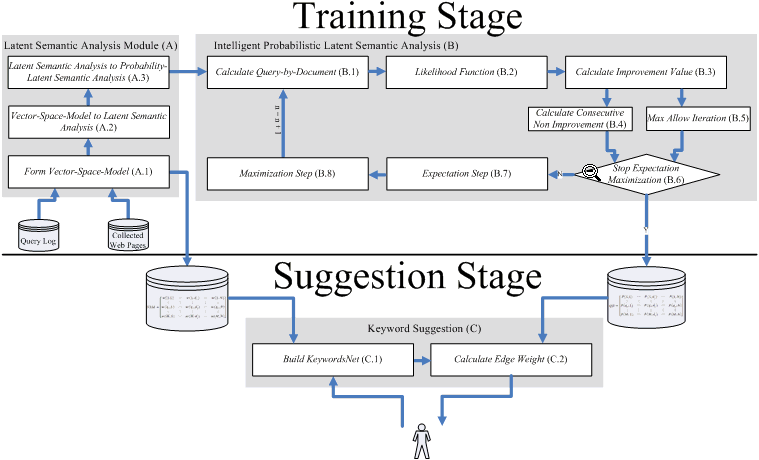
The main objective of this module (marked 'A' in the figure) is to use the latent semantic analysis probability model to form the initial parameters. This model is based on a dual 'latent semantic analysis-and-probabilistic latent semantic analysis' probability model developed by Ding (2005) and Bellegarda (2008). We must accomplish the following three tasks to form this model: (a) use terms and documents to form a vector-space-model matrix; (b) use the result of the vector-space-model matrix to form the relevant latent semantic analysis parameters; and (c) transform these latent semantic analysis parameters into the latent semantic analysis probability model. All the above-mentioned three tasks are corresponding to "Form Vector-Space-Model", "Vector-Space-Model to Latent Semantic Analysis", and "Latent Semantic Analysis to Probability-Latent Semantic Analysis" sub-modules, respectively, as shown in the following lists.
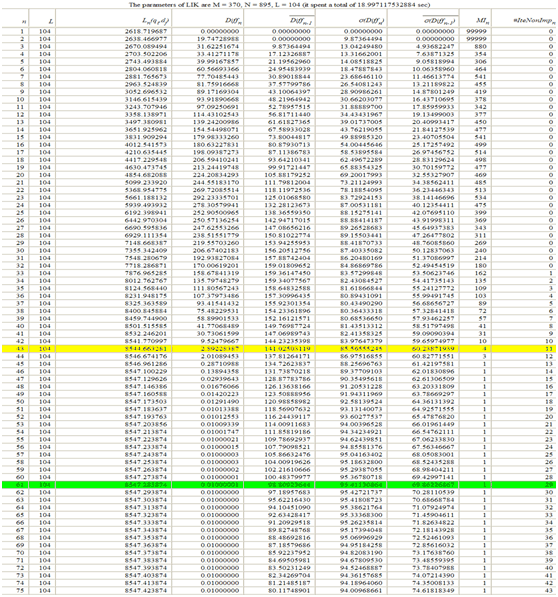
The main task of this sub-module (A.1 in Figure 1) is to calculate the co-occurrence weight in a vector-space-model matrix by a general search engine as shown in Figure 2, where M is all query terms derived from the 'AOL Query Log' and N is all the collected Web pages.
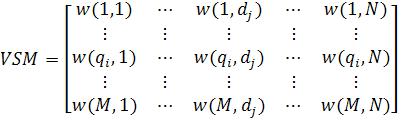
Currently, the element of the matrix, w(qi,dj), is using an SVV algorithm (Chen and Luh 2005) to calculate its weight. SVV is based on the primacy effect of browsing behaviour (Lempel and Moran 2000; Morris and Maisto 2001; Paepcke et al. 2000), that is, the users prefer top ranking items in the search results and this preference gradually decreases. Based on the above observation, we first defined a user behaviour function (Chen and Luh 2005) to state this effect, as shown in the following equation:
where α denotes the degree of the user preference for the first item; lobj denotes the relative order of the object obj within an ordered item list l; and β denotes the decline degree of the user preference.
According to user behaviour function's definition, we then defined w(qi,dj) based on the dot product between different user behaviour functions that are derived from various search engines, as shown in the following equation:
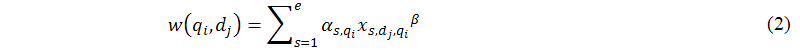
where e is the number of search engines used in SVV; s is a search engine number; αs,qi is the degree of the user preference for the first listing returned from search engine s in response to the user's query qi; xs,dj,qi is the relative order of a Web page dj within the search listings x returned from s in response to qi; and β is the decline degree of the user preference. According to the definition of equation (2), we know that a Web page has a larger weight if it either wins more votes from different search engines or ranks high in the listings of at least one search engine. More details of SVV are described in our previous work (Chen and Luh 2005).
The main task of this sub-module (A.2 in Figure 1) is to convert the vector-space-model matrix into the relevant latent semantic analysis parameters. Latent semantic analysis is an important information retrieval technique, which is used to solve the problem of synonymy. Latent semantic analysis finds a low-rank approximation matrix, which is smaller and less noisy than the vector-space-model matrix. For a fixed k, using a truncated singular value decomposition technique, which conserves k largest singular values and sets others tobe zero, to approximate the vector-space-model matrix, as shown in the following equation:
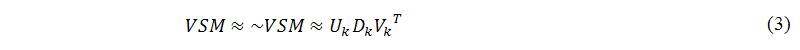
where Dk=diag(σ1,σ2,...,σk) is a k*k diagonal matrix, which contain the singular value of the vector-space-model matrix arranged in decreasing order; Uk=(u1,u2,...,uk) is a M*k left singular matrix, which is a unitary matrix; and Vk=(v1,v2,...,vk) is a N*k right singular matrix, which is also a unitary matrix.
The main task of this sub-module (A.3) is to transform the relevant latent semantic analysis parameters, Uk, Dk, and Vk into the latent semantic analysis probability model that provides the initial parameters.
Although probabilistic latent semantic analysis can converge to the local optimal solution (Hofmann 2001), its result is closely related to how one decides which methods are appropriate to initialize its parameters. According to literature reviews (Brants 2005; Brants and Stolle 2002), the initial parameters of probabilistic latent semantic analysis can be determined by using either random initialization or according to some prior knowledge.
Hofmann (2001) proposed a dual model to express the relationship of latent semantic analysis and probabilistic latent semantic analysis. This model uses the parameters of probabilistic latent semantic analysis to estimate the relevant latent semantic analysis parameters, as shown in the following equations:



where P(qi|zk), P(zk), and P(dj|zk) are all probabilistic latent semantic analysis parameters, as described in section 3.1.2. After viewing equations (4) to (6), we can determine the initial parameters of probabilistic latent semantic analysis according to the result of singular value decomposition.
However, singular value decomposition may introduce negative values in the elements of Uk and Vk matrices, and such values cannot be treated as a probability distribution. Thus, we cannot directly use the result of singular value decomposition to be the initial parameters.
To solve the problem of negative values in singular value decomposition, Ding (2005) and Bellegarda (2008) used a dual probability model to estimate the elements of Uk and Vk, as shown in the following equations, where uk and vk are the left and right singular vectors, respectively:
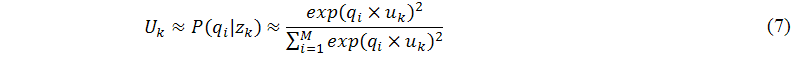
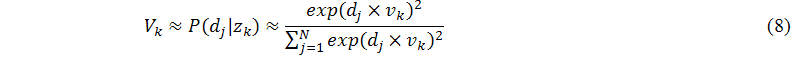
Moreover, according to the definition of singular value decomposition, we know that the singular values of the vector-space-model matrix, σk, are all larger than zero. Thus, we use a probability form to estimate the elements of Dk, as shown in the following equation:
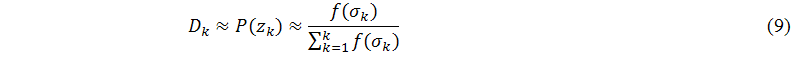
where f(σk) is any non-decreasing function and its value is larger than zero. According to the definition of singular value decomposition, σi≥σi+1>0 where i≥1, we can guarantee f(σi)≥f(σi+1)>0. Below, we will simulate three non-decreasing functions to verify that different f(σk) functions how to affect the value of the objective function, as described in the following lists:
The main objective of this module (B) is to generate the training parameter, called query-by-document matrix, which is then used for the suggestion stage. The basis of this module is the probabilistic latent semantic analysis developed by Hofmann (1999).
To effectively generate the query-by-document matrix, we must accomplish the following two tasks: (a) adopt the probabilistic latent semantic analysis method to generate the query-by-document matrix and (b) use an adaptive mechanism to reduce the number of iterations required to run probabilistic latent semantic analysis. In the first task, we use the sub-modules calculate query-by-document, likelihood function, expectation step, and maximization step to generate the query-by-document matrix. In the second task, we use the sub-modules of calculate improvement value, calculate consecutive non-improvement, max allow iteration and stop expectation maximization to determine whether probabilistic latent semantic analysis should be terminated or not. All the above-mentioned sub-modules are shown in the following lists.
The main task of this sub-module (B.1) is to form the query-by-document matrix, as shown in Figure 3, based on the observed data.
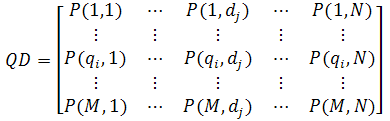
Probabilistic latent semantic analysis applies a probabilistic aspect model to derive the element of the matrix, called P(qi,dj). Probabilistic latent semantic analysis assumes that term qi and document dj exist as a series of latent topics Z={z1,...,zk,...,zL}, where L is the total number of topics. To calculate P(qi,dj), we first need to define the relevant parameters in the following lists:
Based on the parameters above, we now calculate the joint probability of an observed pair (qi,dj) by summing over all possible choices of Z={z1,...,zk,...,zL} from which the observation could have been generated (it is clearly shown in Figure 4(a)), as shown in the following equation:
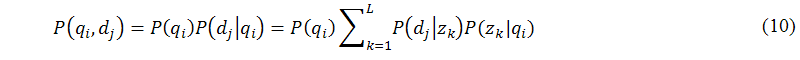
Then, by applying Bayes's rule, it is straightforward to transform equation (10) into the following form (it is clearly shown in Figure 4(b)), as shown in the following equation:
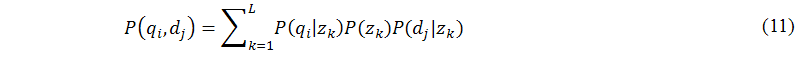
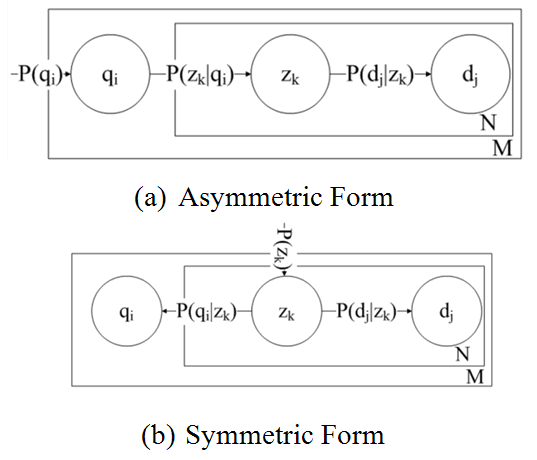
The main task of this sub-module (B.2) is to calculate the value of the likelihood function L. To calculate the joint probability of an observed pair (qi,dj), probabilistic latent semantic analysis follows the likelihood principle to estimate the parameters P(qi|zk), P(zk), and P(dj|zk) by maximization of the likelihood function Ln(qi,dj) at iteration n, as shown in the following equation:
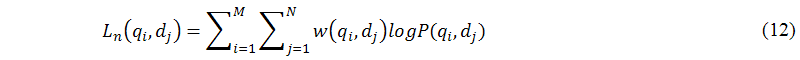
The main task of this sub-module (B.7) is to achieve the expectation step of the expectation maximization algorithm. The expectation maximization algorithm (Dempster et al. 1977) is a well-known method to perform maximum likelihood parameter estimation in latent variable models. Generally, the expectation and maximization steps are needed to perform in this algorithm alternately. In the expectation step, probabilistic latent semantic analysis can simply apply Bayes's formula to generate the latent variable zk based on the current estimates of the parameters qi and dj as follows:
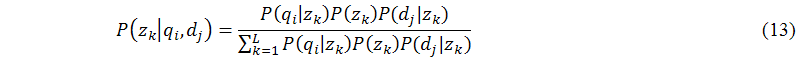
The main task of this sub-module (B.8) is to achieve the maximization step of the expectation maximization algorithm. In the maximization step, probabilistic latent semantic analysis applies the Lagrange multipliers method (see (Hofmann 2001) for details) to solve the constraint maximization problem to get the following equations for re-estimated parameters P(qi|zk), P(zk), and P(dj|zk) as follows:
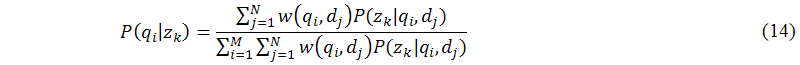
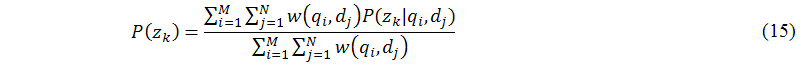
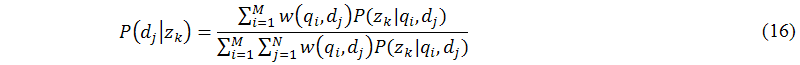
Now, either intelligent probabilistic latent semantic analysis can substitute equations (7) to (9) or equations (14) to (16) into equations (11) and (12) until the termination criteria are reached.
The main task of these sub-modules is to develop a performance-based termination criterion. This termination criterion can drastically reduce the number of iterations required to run at this stage, and it should be able to produce the training parameter relatively quickly.
Probabilistic latent semantic analysis is a time consuming and expensive process for each iteration and is related to the convergence speed of the expectation maximization algorithm (Tsoi 2001). Dempster et al. (1977) proved that the log-likelihood function is monotonically increasing until the local optimal solution is reached. Hofmann (2004) proved that the time complexity is O(M*N*L), where O(M*N) is the time complexity of the expectation maximization algorithm for each iteration.
However, in the information retrieval environment, the total number of query terms (M) and the total number of Web pages (N) are both large. Moreover, the total number of topics (L) is increased along with increased M and N (Inoue 2005). According to the observation of Kunder (2008), the number of query terms and Web pages is enormous and the number of Web pages is still increasing, and this situation might will result in system performance being quite disappointing when probabilistic latent semantic analysis is applied to solve various large-scale information retrieval problems.
Thus, we must design an effective mechanism that skilfully balances cost (the number of iterations required to run) and performance (the value of the log-likelihood function). In this mechanism, we use the log-likelihood function (equation 12) to define the termination criteria (the stop expectation maximization sub-module), which are not only to converge to the local optimal solution, but also the maximum required number of iterations is reached. We discuss these two criteria below.
In the first criterion, we define that the local optimal solution is reached if the improvement value between two consecutive iterations is less than a predefined threshold. We let Diffn be the improvement value of the log-likelihood function at the nth iteration (calculate improvement value sub-module), as shown in the following equation:
We then define the local optimal solution as shown in the following equation, where ε denotes the predefined threshold of the first criterion.
In the second criterion, the maximum required number of iterations is usually set as a fixed number through experiments. However, it is a difficult task to claim what the maximum required number of iterations should be. On the one hand, a large number of iterations may waste a significant amount of computing resources on a relatively small improvement. On the other hand, a small number iterations may result in the difference being large, compared with the final solution and the local optimal solution. It will be a cost-effective solution if the maximum required number of iterations is dynamically determined according to a case of real improvement for each iteration.
We then formally define the second criterion as follows: the consecutive number of iterations without improvement is larger than the maximum allowable number of iterations without significant improvement at current iteration. We consider that is a sign that further computation could not yield much progress.
The second criterion must define two important curves, one for the increasing cost curve and the other one for the decreasing performance curve. This criterion is fulfilled if there exists an iteration n such that the value of the cost curve is larger than the value of the performance curve. In the cost curve at iteration n #IteNonImpn, the consecutive number of iterations without improvement (calculate consecutive non-improvement sub-module), is defined as the following equation:
where avg(Diffn-1) denotes the average of all Diffs, 1≤s≤n-1. That is, the nth iteration is said to make no improvement if Diffn < avg(Diffn-1). Next, in the performance curve at iteration n MIn, the maximum allowable number of iterations without significant improvement (max allow iteration sub-module), is defined as the following equation:
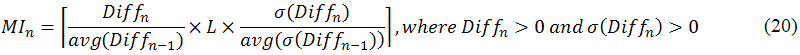
where L denotes the total number of topics; σ(Diffn) denotes the standard deviation of all Diffs, 1≤s≤n-1; avg(σ(Diffn-1)) denotes the average of all σ(Diffs). As indicated in the definition of equation (20), the performance curve MIn is dynamically determined based on the ratio of improvement history progress Diffn/avg(Diffn-1) and the ratio of variation history progress σ(Diffn)/avg(σ(Diffn-1)). If either Diffn/avg(Diffn-1) or σ(Diffn)/avg(σ(Diffn-1)) is large, there is a significant progress or variation progress in the log-likelihood function. Finally, let us formally define the second criterion as follows:
The main objective of this stage is using the query-by-document matrix to generate the desirable result of our system by a keyword suggestion module. To suggest the relevant keywords, this stage first constructs a semantic graph. Then, it transforms the query-by-document matrix into the edge weight of each directed edge in the graph. Finally, it is sorting a list of suggested keyword according to the edge weight.
This main objective of this module ('C' in figure 1) is to adopt breadth-first-search and the concept of inverse link to build a semantic graph, called KeywordsNet and then this graph is applied to generate a list of suggested keywords.
To generate a list of suggested keywords and the degree of similarity between the user's query and each suggested keyword, we must accomplish the following two tasks: (a) build a KeywordsNet and (b) transform the query-by-document matrix into the edge weight of KeywordsNet. These two tasks are corresponding to the build KeywordsNet and calculate edge weight sub-modules, as shown in the following lists.
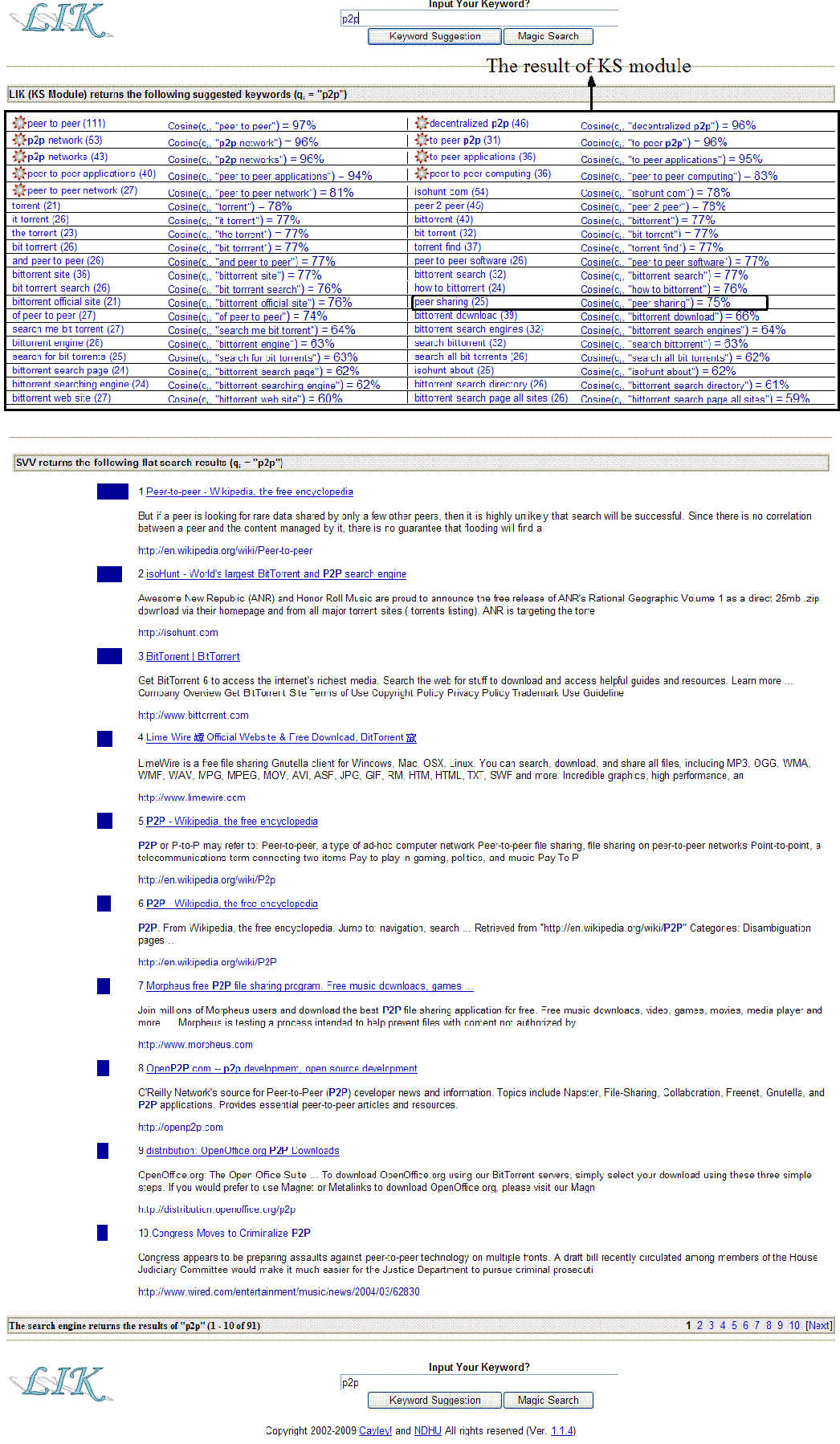
The main task of this sub-module (C.1) is to build a KeywordsNet graph based on breadth-first-search and the concept of inverse link. In the graph, based on a user query qi, nodes represent all candidate keywords qkss, and each directed edge (qi,qks) between qi and qks represents these two keywords exist in a strong semantic relationship and qks is suggested from qi. Figure 5 is a partial KeywordsNet graph to illustrate the strong semantic relationships between p2p and some candidate keywords.
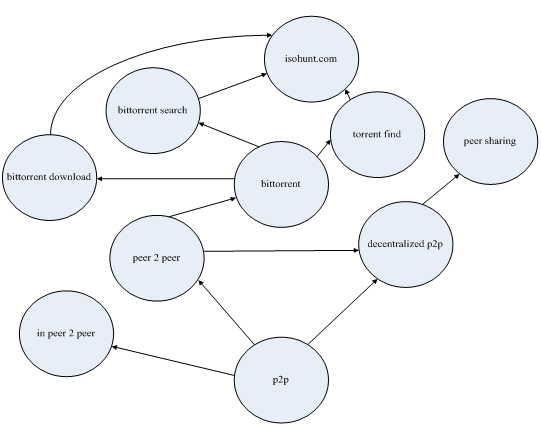
Definition (strong semantic relationship): qi and qks exist in a strong semantic relationship feature and (qi,qks) is a directed edge if and only if these two keywords satisfy at least one of the following three relationships: (1) equivalence, (2) hierarchy, and (3) association (NISO 2005). If there is an equivalent relationship between qi and qks, these two keywords are expressing the same concept. If qi and qks can obtain a parent-child relationship through an intermediate candidate keyword, these two keywords have a hierarchical relationship. If qi and qks can obtain an ancestor-descendant relationship through a series of intermediate candidate keywords, these two keywords have an association relationship. Note that we only show the directed edges of the equivalence relationship to prevent needlessly complex in Figure 5.
The main assumption of KeywordsNet is that if many important candidate keywords link to an important Web page, it can use the inverted index of the vector-space-model matrix to identify these important candidate keywords. KeywordsNet uses a series of recursive breadth-first-search calls to form a strong semantic relationship feature, as shown in the following pseudo code.
- Algorithm Breadth-First-Search(qi as string, PathLength as integer)
- {
- If (PathLength>MaxLen)
- Return(KeywordsNetGraphqi);
- Else {
- D=Fetch all important Web pages corresponding to qi;
- Foreach (D as dj) {
- ImportantKEYS=Use the inverted index of dj listed in the vector-space-model matrix to identify all important candidate keywords corresponding to qi;
- Foreach (ImportantKEYS as qks) {
- KeywordsNetGraphqi+=(qi,qks);
- Breadth-First-Search(qks, PathLength+1);
- } End of Foreach
- } End of Foreach
- } End of Else
- } End of Algorithm
In the first recursive call, qi generates a candidate keyword qks(1). Hence, qi is equivalent to qks(1) since they share a same concept (Web page) dj. In the second recursive call, qks(1) generates a candidate keyword qks(2). Hence, qi and qks(2) exist in a hierarchical relationship since the child candidate keyword qks(2) can be accessed from the parent candidate keyword qi through an intermediate candidate keyword qks(1). In the tth (1 < t ≤ MaxLen) recursive call, qks(t-1) generates a candidate keyword qks(t). Hence, qi is associated with qks(t) since there is a shortest path whose length is t from qi to qks(t).
Example 1 (build a partial keywordsNet)
In examples 1 and 2, we assume that the query terms are q1=p2p", q2=peer to peer, q3=in peer to peer, q4=bittorrent, q5=torrent find and the collected Web pages are d1=en.wikipedia.org/wiki/Peer-to-peer, d2=www.bittorrent.com, d3=isohunt.com. Figure 6 shows an example of the vector-space-model matrix by using our SVV algorithm.
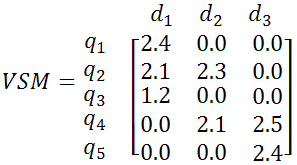
The main task of this sub-module (C.2) is to transform the query-by-document matrix into the edge weight of KeywordsNet. We use a cosine similarity metric (Salton 1989; Zhang and Nasraoui 2008) to achieve this transformation process, as shown in the following equation:
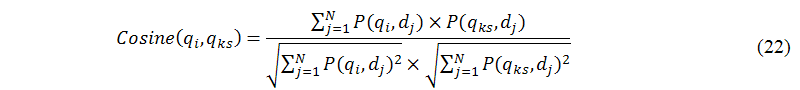
where P(qx,dj), x∈{i,ks}, denotes the element of the query-by-document matrix, which is the joint probability of an observed pair (qx,dj) derived from the training stage. All suggested keywords with the degree of similarity are shown in sorted order according to the edge weight. Additionally, we also discard such keywords whose directed edges with a relative small edge weight. For example, in Figure 7, the degree of similarity for the directed edge (p2p, peer sharing) is 75% (Cosine(p2p, peer sharing)=75%).
Example 2 (suggest keywords with the degree of similarity)
According to the results of example 1, the directed edges are (q1,q2), (q1,q3), (q1,q4) and (q1,q5) for the seed keyword q1. Figure 8 shows an example of the result of the query-by-document matrix by the modules of latent semantic analysis and intelligent probabilistic latent semantic analysis.
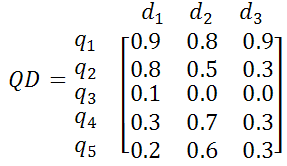
In Table 2, we list the edge weight for each directed edge by adopting equation (22). Finally, the directed edge (q1,q3) should be discarded since it is a directed edge with a relatively small edge weight.
| Directed edge | (q1, q2) | (q1, q3) | (q1, q4) | (q1, q5) |
| Edge weight | 93.40% | 59.87% | 89.39% | 88.38% |
| Discard | X |
In this section, we present three experiments to illustrate the performance comparison between different systems and the relevant parameters considered in our system. First, we present the performance comparisons between our system and other systems. Second, we verify that the performance of the latent semantic analysis probability model is better than the random probability model. Third, we also verify that the termination criteria of intelligent probabilistic latent semantic analysis can yield a cost effective solution within a controlled period of time.
In this experiment, we pay attention to how to rate the performance of different systems compared with CatS, Highlight, Credo, Carrot2,Google Proximity Search, Google AdWords, Yahoo Search Marketing, Clusty, WordTracker, and LIK. All the systems except LIK are described in section 2.1. On the one hand, we evaluate the performance of these systems by a simulation and a user evaluation studies. On the other hand, we also simulate the performance of the training parameter generated from different models to verify that which step in the training stage has a major impact on the quality of our system.
In this experiment, we randomly selected 1,000 query terms from Dogpile (InfoSpace 2008), which people were using to search the Internet. The 1,000 random query terms were listed in (Dogpile 2008).
To compare the performance of different systems for our simulation program, we need to define a new performance metric, DIST, to fairly measure the average distance between the seed keyword qi and any one of suggested keywords qks when the number of qi is 1, as shown in the following equation:
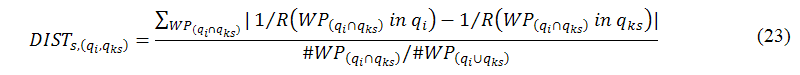
where WP(qi∩qks) (WP(qi∪qks)) is the intersection (union) of the top ten Web pages returned from qi and qks when the search engine s is used to measure; R(WP(qi∩qks) in qx), x∈{i,ks}, is the ranking of WP(qi∩qks) in response to qx if R(WP(qi∩qks) in qx)>0, and 1/R(WP(qi∩qks) in qx)=0 if WP(qi∩qks) cannot be found in qx.
The motivation of this study is to minimize the average distance between qi and qks. Equation (23) implies the following three important properties. First, the number of WP(qi∩qks) is comparatively large, which implies that the Web pages returned from qi and qks are close to each other. Second, the value of |1/R(WP(qi∩qks) in qi) - 1/R(WP(qi∩qks) in qks)| is much less, which implies that the rankings of WP(qi∩qks) appearing in qi and qks are similar. Third, the front rankings of WP(qi∩qks) have greater impact on DIST than the rear rankings, which implies that the dominant factor of DIST is the ranking of WP(qi∩qks).
We then use MDIST to measure the average distance between qi and all suggested keywords when the number of qi is 1, as shown in the following equation:
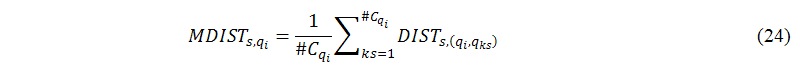
where Cqi is all suggested keywords returned from qi. We set the number of Cqi (#Cqi) equal to 10 to save the simulation time. That is, we calculate the average distance between qi and the top 10 suggested keywords. Figure 9 shows the distribution of MDISTSVV,qi
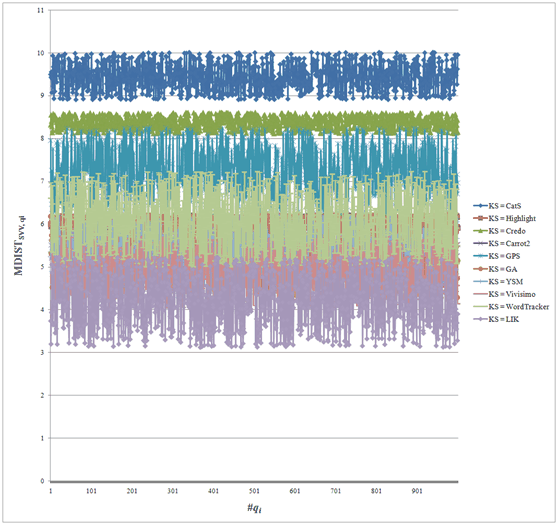
For comparison purpose, we average all MDISTSVV,qi when the number of qi is 1000, as shown in Table 3. We found that the average score of MDISTSVV,qi obtained from LIK is 4.214660, which implies that it generates the suggested keywords with the minimal average distance score. Table 3 also shows the average score of MDISTs,qi when Google and Yahoo are used to measure. No matter which search engines are used to measure, the average score of MDISTs,qi for LIK is lowest that implies that the performance of our system is best.
| System | Average MDISTSVV,qi | Average MDISTGoogle,qi | Average MDISTYahoo,qi |
| CatS | 9.452357 | 9.466205 | 9.439944 |
| Highlight | 6.013398 | 6.015043 | 6.016055 |
| Credo | 8.365567 | 8.362261 | 8.359115 |
| Carrot2 | 5.412458 | 5.420196 | 5.414073 |
| Google Proximity Search | 7.242496 | 7.250456 | 7.235417 |
| Google AdWords | 5.252066 | 5.275507 | 5.281719 |
| Yahoo Search Marketing | 5.245478 | 5.256330 | 5.282105 |
| Clusty | 4.893964 | 4.886279 | 4.844971 |
| WordTracker | 6.103158 | 6.115633 | 6.138991 |
| LIK | 4.214660 | 4.143232 | 4.164376 |
Next, we also simulate the training parameter generated from which step in the training stage that has a major impact on the performance of our system. In this simulation, we mainly compare the performance of the models of non-latent semantic analysis, latent semantic analysis, latent semantic analysis-prob, and probabilistic latent semantic analysis, that is, we use the results of the vector-space-model matrix (non-latent semantic analysis), singular value decomposition (latent semantic analysis), dual-probability (latent semantic analysis-prob), and expectation maximization (probabilistic latent semantic analysis), respectively, as the element of the query-by-document matrix. Table 4 shows the average score of MDISTs,qi when SVV, Google, and Yahoo are used to measure.
| Model | Average MDISTSVV,qi | Average MDISTGoogle,qi | Average MDISTYahoo,qi |
| Non-Latent Semantic Analysis | 5.512683 | 5.562672 | 5.501257 |
| Latent Semantic Analysis | 4.912361 | 4.812367 | 4.851436 |
| Latent Semantic Analysis-Prob | 5.134633 | 5.150166 | 5.114612 |
| Probabilistic Latent Semantic Analysis" | 4.635162 | 4.602481 | 4.612465 |
According to Table 4, we found that the training parameter generated from probabilistic latent semantic analysis has the lowest average MDIST score, which means that probabilistic latent semantic analysis has a major impact on the performance of our system. The average score of probabilistic latent semantic analysis is superior to latent semantic analysis since it can provide a better polysemy capability against latent semantic analysis. That is, the keywords suggested from probabilistic latent semantic analysis have more polysemous means than latent semantic analysis, and thus, we use the result of probabilistic latent semantic analysis as the core step of our system.
Although latent semantic analysis-prob takes more computer time than latent semantic analysis, because it is derived from the result of latent semantic analysis, the performance of latent semantic analysis-prob" is worse than latent semantic analysis because it uses a probability form to estimate the result of latent semantic analysis and it certainly results in a small amount of noise from this estimation process. In our system, the latent semantic analysis-prob model is a bridge connecting latent semantic analysis to probabilistic latent semantic analysis. We cannot directly use the result of latent semantic analysis as the initial parameters since singular value decomposition may introduce negative values in the result of latent semantic analysis and such values cannot be treated as a probability distribution. Therefore, we use the result of latent semantic analysis-prob as the initial parameters.
Finally, we selected thirty-nine of the most searched query terms in 2007 from Google (2007), Yahoo (Saremi 2007) and Lycos (2007) that belonging to many different topics (anna nicole smith, badoo, beyonce, britney spears, club penguin, dailymotion, disney, ebuddy, facebook, fantasy football, fergie, fifa, golf, heroes, hi5, iphone, jessica alba, kazaa, lindsay lohan, Mozart, mp3, myspace, naruto, paris hilton, pokemon, poker, rebelled, rune scape, second life, shakira, sudoku, tmz, transformers, webdetente, webkinz, world cup, wwe, xanga, youtube), and asked to thirty undergraduate and six graduate students from National Dong Hwa University to compare the results of different systems.
For each of the thirty-nine query terms, the thirty-sex users computed the precision at the first N suggested keywords associated with the query terms generated by each system. Precision at top N is defined as
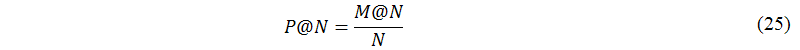
where M@N is the number of suggested keywords that have been manually tagged as relevant among the first N suggested keywords computed by each system.
The results of the experiment for P@3 are shown in Table 5. The number in each percentage cell (except the last row) is the average P@3 score of each system on a given evaluated query for thirty-six users. For example, CatS has an average P@3 score of 49.3% when the query is anna nicole smith. The number in the last row is the average P@3 score of each system on all evaluated query terms for thirty-six users.
| Query terms | CatS | Highlight | Credo | Carrot2 | Google Proximity Search | Google AdWords | Yahoo Search Marketing | Clusty | WordTracker | LIK |
| anna nicole smith | 49.3% | 76.9% | 63.5% | 72.3% | 67.7% | 75.2% | 82.3% | 82.3% | 76.1% | 82.7% |
| badoo | 42.7% | 75.2% | 58.1% | 76.0% | 68.6% | 84.0% | 78.3% | 76.6% | 76.5% | 91.2% |
| beyonce | 44.3% | 73.9% | 60.7% | 80.4% | 61.9% | 80.4% | 81.6% | 82.3% | 66.3% | 83.3% |
| britney spears | 45.6% | 68.3% | 64.6% | 71.7% | 62.2% | 83.3% | 73.3% | 81.8% | 69.7% | 84.7% |
| club penguin | 56.4% | 67.6% | 64.7% | 82.3% | 64.3% | 74.5% | 77.3% | 81.8% | 66.8% | 82.7% |
| dailymotion | 56.6% | 70.1% | 61.9% | 75.1% | 66.4% | 83.8% | 79.2% | 77.1% | 68.4% | 86.6% |
| disney | 55.3% | 71.1% | 56.0% | 83.2% | 62.2% | 85.1% | 80.5% | 79.5% | 68.5% | 93.6% |
| ebuddy | 56.0% | 74.1% | 62.9% | 73.1% | 64.3% | 82.4% | 80.0% | 79.9% | 74.1% | 93.3% |
| 46.3% | 69.8% | 55.9% | 80.5% | 66.8% | 83.4% | 78.1% | 77.4% | 74.6% | 87.5% | |
| fantasy football | 53.7% | 76.2% | 56.4% | 77.3% | 69.1% | 79.8% | 77.3% | 81.3% | 69.7% | 94.0% |
| fergie | 46.1% | 72.5% | 59.0% | 79.4% | 65.6% | 76.2% | 75.8% | 84.9% | 65.6% | 84.3% |
| fifa | 43.6% | 74.5% | 65.4% | 80.2% | 61.9% | 85.0% | 84.9% | 82.0% | 75.8% | 87.6% |
| golf | 57.6% | 76.0% | 62.3% | 71.9% | 65.5% | 73.2% | 81.6% | 77.6% | 75.5% | 85.0% |
| heroes | 52.5% | 72.8% | 60.5% | 76.2% | 62.8% | 81.6% | 74.5% | 80.8% | 66.9% | 91.2% |
| hi5 | 50.8% | 70.5% | 56.6% | 71.9% | 69.0% | 76.4% | 75.2% | 79.5% | 69.9% | 88.5% |
| iphone | 48.4% | 75.1% | 55.9% | 71.5% | 63.6% | 75.3% | 83.6% | 81.2% | 66.8% | 84.1% |
| jessica alba | 55.1% | 73.2% | 56.0% | 83.2% | 69.1% | 81.7% | 76.7% | 79.6% | 68.4% | 91.4% |
| kazaa | 48.0% | 73.3% | 62.7% | 81.3% | 66.8% | 75.8% | 81.3% | 82.8% | 73.8% | 85.7% |
| lindsay lohan | 56.3% | 70.4% | 55.9% | 75.6% | 62.0% | 75.6% | 82.8% | 78.4% | 73.9% | 94.0% |
| mozart | 49.9% | 67.7% | 58.2% | 80.3% | 67.0% | 77.6% | 75.2% | 80.7% | 65.5% | 85.7% |
| mp3 | 56.0% | 76.1% | 58.6% | 78.1% | 61.4% | 84.3% | 77.5% | 77.9% | 74.3% | 82.1% |
| myspace | 47.9% | 75.1% | 60.4% | 78.4% | 67.8% | 74.7% | 74.6% | 83.6% | 71.9% | 93.2% |
| naruto | 48.6% | 71.9% | 58.2% | 80.1% | 61.5% | 74.6% | 78.1% | 81.9% | 71.2% | 83.2% |
| paris hilton | 43.7% | 74.1% | 60.0% | 82.9% | 65.3% | 83.1% | 79.0% | 82.0% | 71.8% | 93.4% |
| pokemon | 55.9% | 68.8% | 60.9% | 81.2% | 67.1% | 83.9% | 83.1% | 81.4% | 65.9% | 86.7% |
| poker | 43.8% | 75.3% | 59.9% | 74.7% | 63.9% | 82.2% | 82.2% | 84.7% | 72.7% | 85.7% |
| rebelde | 43.0% | 71.2% | 65.5% | 71.9% | 65.8% | 79.6% | 78.1% | 78.9% | 71.0% | 93.0% |
| rune scape | 47.7% | 68.4% | 64.5% | 81.5% | 64.6% | 78.4% | 84.6% | 84.4% | 75.9% | 88.4% |
| second life | 56.0% | 76.2% | 63.1% | 83.1% | 68.3% | 77.7% | 77.3% | 79.9% | 74.9% | 85.8% |
| shakira | 55.7% | 70.7% | 62.9% | 72.4% | 67.5% | 82.7% | 82.9% | 86.8% | 68.0% | 83.2% |
| sudoku | 57.6% | 72.7% | 61.0% | 73.2% | 63.8% | 75.8% | 80.6% | 80.9% | 70.1% | 92.5% |
| tmz | 42.8% | 75.4% | 57.5% | 76.0% | 69.0% | 84.5% | 85.0% | 83.0% | 72.3% | 82.3% |
| transformers | 50.5% | 75.8% | 63.2% | 79.0% | 64.2% | 81.6% | 75.2% | 78.8% | 69.4% | 93.8% |
| webdetente | 55.0% | 74.8% | 59.2% | 74.3% | 64.9% | 84.8% | 77.1% | 85.3% | 76.3% | 84.3% |
| webkinz | 55.7% | 73.6% | 60.0% | 82.3% | 68.3% | 78.5% | 81.7% | 78.4% | 66.1% | 90.2% |
| world cup | 55.6% | 69.3% | 56.6% | 80.6% | 62.4% | 76.5% | 84.2% | 78.7% | 66.4% | 85.6% |
| wwe | 43.8% | 73.8% | 57.5% | 76.6% | 63.7% | 83.0% | 80.6% | 84.4% | 76.2% | 89.3% |
| xanga | 49.4% | 73.0% | 56.9% | 76.1% | 66.8% | 79.4% | 75.4% | 78.2% | 73.3% | 91.3% |
| youtube | 53.7% | 73.1% | 55.9% | 74.6% | 68.2% | 77.0% | 79.0% | 78.8% | 66.0% | 82.6% |
| Average | 50.7% | 72.8% | 60.0% | 77.4% | 65.4% | 79.8% | 79.4% | 80.9% | 70.9% | 87.8% |
The average scores of CatS, Highlight, Credo, Carrot2,Google Proximity Search, Google AdWords, Yahoo Search Marketing, Clusty, WordTracker and LIK for P@3 are 50.7%, 72.8%, 60.0%, 77.4%, 65.4%, 79.8%, 79.4%, 80.9%, 70.9%, and 87.8%, respectively. Moreover, we have extended this analysis to the analyses of P@5, P@7, and P@10, as shown in Table 6.
| Average P@N | CatS | Highlight | Credo | Carrot2 | Google Proximity Search | Google AdWords | Yahoo Search Marketing | Clusty | WordTracker | LIK |
| Average P@3 | 50.7% | 72.8% | 60.0% | 77.4% | 65.4% | 79.8% | 79.4% | 80.9% | 70.9% | 87.8% |
| Average P@5 | 47.0% | 69.1% | 57.2% | 72.2% | 60.9% | 75.2% | 75.4% | 77.9% | 67.0% | 85.5% |
| Average P@7 | 42.2% | 62.9% | 51.3% | 68.9% | 56.5% | 70.1% | 69.9% | 73.1% | 62.5% | 79.6% |
| Average P@10 | 35.7% | 58.0% | 45.2% | 61.8% | 50.6% | 64.6% | 64.6% | 66.0% | 55.9% | 74.6% |
We then used SPSS 11.0 for Windows to analyse the results of above experiment. Considering the performance of CatS, Highlight, Credo, Carrot2,Google Proximity Search, Google AdWords, Yahoo Search Marketing, Clusty, WordTracker, and LIK. We used the statistical methodology, ANOVA analysis, to show that F(PR@3)=386.443, F(PR@5)=470.596, F(PR@7)=463.473, and F(PR@10)=496.528 (Table 7) are all greater than F0.001(9,380)=2.454 (F-distribution). This provides extremely strong evidence against the null hypothesis, indicating that there is a significant difference in the performance of different systems on the user's evaluation.
| Sum of Squares | Degree of Freedom | Mean Square | F | Sig. | ||
| PR@3 | Between Groups | 4.348 | 9 | 0.483 | 386.443 | 0 |
| Within Groups | 0.475 | 380 | 0.001 | |||
| Total | 4.823 | 389 | ||||
| PR@5 | Between Groups | 4.417 | 9 | 0.491 | 470.596 | 0 |
| Within Groups | 0.396 | 380 | 0.001 | |||
| Total | 4.814 | 389 | ||||
| PR@7 | Between Groups | 4.367 | 9 | 0.485 | 463.473 | 0 |
| Within Groups | 0.398 | 380 | 0.001 | |||
| Total | 4.765 | 389 | ||||
| PR@10 | Between Groups | 4.520 | 9 | 0.502 | 496.528 | 0 |
| Within Groups | 0.384 | 380 | 0.001 | |||
| Total | 4.905 | 389 | ||||
We conducted a post hoc Fisher's least significant difference for pair-wise comparison at the 1% significance level. Because the results of least significant difference are tedious, we refer readers to the full report (LIK 2009). As illustrated in the results of least significant difference, our system was found to overwhelmingly better than other systems.
For a large part of the query terms, the users did not like CatS since it suggests keywords that only show the category names that derived from the dmoz taxonomy. Credo only suggests keywords with a single term. Highlight obtains the top-level suggested keywords by using a classification technology, so that they are few and of little use.Google Proximity Search, WordTracker, Google AdWords, and Yahoo Search Marketing are failing to suggest any keywords that do not contain the seed keyword. Although Carrot2 and Clusty can create the suggested keywords with a semantic feature, however, they only use a pattern matching technique to analysis the Web snippet returned from different search engines. That is, they will fail to suggest the keywords if it do not appear in the Web snippet. Our system uses the methods of latent semantic analysis and probabilistic latent semantic analysis to construct the latent topics from the vector-space-model matrix and the suggested keywords are all based on these results. Thus, our system can guarantee any suggested keywords that have a synonymy or polysemy feature with the seed keyword. Moreover, our system can suggest the keywords with an association relationship since it uses a graph search method to derive the candidate keywords from a semantic graph. For example, in Figure 7, our system can suggest the keyword isohunt.com (the most comprehensive bit torrent search engine) when the seed keyword is p2p.
In this experiment, we use the random and latent semantic analysis probability models to compare the performance of the log-likelihood function as described in equation (12) in order to decide the initial parameters.
The random probability model, RAND, uses a random probability as the initial parameters. The latent semantic analysis probability model first uses singular value decomposition to transform the vector-space-model matrix into the relevant latent semantic analysis parameters, then it uses a dual probability model to transform the relevant latent semantic analysis parameters into the initial parameters. According to the definition of the function f(σk) in equation (9), the latent semantic analysis probability model can be divided into three submodels: (1) f(σk)=exp(σk) (latent semantic analysis-prob_1), (2) f(σk)=sinh-1(σk) (latent semantic analysis-prob_2), and (3) f(σk)=σk (latent semantic analysis-prob_3).
Hofmann (2004) concluded that three parameters, M (the total number of query terms), N (the total number of Web pages), and L (the total number of topics), have a major impact on the performance of the log-likelihood function, thus, we experiment with three different cases. Let us now define IRatio for Modelx based on the RAND model where Modelx∈{RAND, latent semantic analysis-prob_1, latent semantic analysis-prob_2, latent semantic analysis-prob_3}, as shown in the following equation:
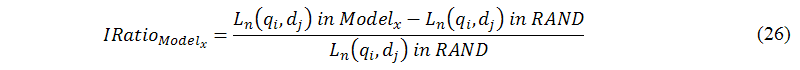
where Ln(qi,dj) in Modelx is the local optimal solution derived from Modelx. The interested readers can simulate this experiment at http://cayley.sytes.net/simulation/init_lik.php.
In the first case, we focus on how to improve IRatio for different L. In this case, we set M=1000, N=1000, and the range of L from 10 to 200. The simulation results for this case are shown in Figure 10 (a). We then average over all IRatios, and the average values for each Modelx are 0% (RAND), 7.38% (latent semantic analysis-prob_1), 7.16% (latent semantic analysis-prob_2), and 7.12% (latent semantic analysis-prob_3), respectively.
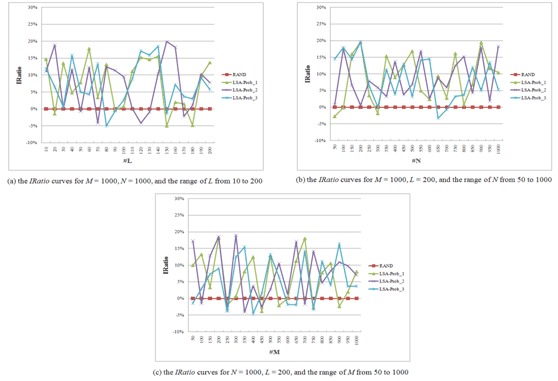
Similarly, in the second and third cases, we focus on how to improve IRatio for different N and M. The simulation results are listed in Figures 10 (b) and (c). We also average over all IRatios for the second case, and the average values for each Modelx are 0% (RAND), 8.69% (latent semantic analysis-prob_1), 8.56% (latent semantic analysis-prob_2), and 8.58% (latent semantic analysis-prob_3), respectively. For the third case, the average values for each Modelx are 0% (RAND), 6.19% (latent semantic analysis-prob_1), 7.23% (latent semantic analysis-prob_2), and 5.24% (latent semantic analysis-prob_3), respectively.
According to above experimental results, we concluded that the performance of the latent semantic analysis probability model is better than the random probability model. Moreover, no matter what experiments are performed, the performances of latent semantic analysis-prob_1, latent semantic analysis-prob_2, and latent semantic analysis-prob_3 are similar, which means that different f(σk) functions will result in a near identical result for the latent semantic analysis probability model.
In this experiment, we pay attention to verify that intelligent probabilistic latent semantic analysis can yield a cost effective solution. The termination criteria have the following two cases: (1) it converges to the local optimal solution or (2) the consecutive number of iterations without improvement exceeds its maximum allowable number of iterations without significant improvement. In this experiment, we randomly chose the following parameters: M (the total number of query terms), N (the total number of Web pages), L (the total number of topics), and w(qi,dj) (the weight of term i in document j). The interested readers can simulate this experiment at http://cayley.sytes.net/simulation/term_lik.php.
The simulation results of two cases are shown in Figure 11, where n is the number of iterations; #IteNonImpn is the consecutive number of iterations without improvement. All other parameters, including Ln(qi,dj), Diffn, avg(Diffn-1), σ(Diffn), avg(σ(Diffn-1)), and MIn are as previously defined.
In the first case, we set ε equal to 0.01, which means that the improvement value of the log-likelihood function at the nth iteration (Diffn) is less than or equal to 0.01. In this simulation, the local optimal solution has already been reached at iteration 61. At this time, we found that the value of the log-likelihood function is 8547.283874.
In the second case, the maximum required number of iterations has already been reached at iteration 43, where the consecutive number of iterations without improvement (#IteNonImpn=11) is larger than the maximum allowable number of iterations without significant improvement (MIn=4). At this time, we found that the value of the log-likelihood function is 8544.663281.
In this simulation, the termination criteria were reached at iteration 43 rather than iteration 61 since it takes additional 18 iterations to increase the value of the log-likelihood function only 2.620593. It means that we perform additional computing resources than the second case, which result in little improvement.
For the second case, we further verify whether our method is a cost effective solution. In this verification, we also simulated 10,000 runs on overall performance improvement, to compare the number of iteration derived from the second case, SYSTEM, with some predefined number of iterations. At each run of this simulation, we also randomly chose the parameters of M, N, L, and w(qi,dj). The predefined number of iterations is based on the local optimal solution that can classify the number of iterations required to run into the following situations: OPTIMAL (local optimal solution), OPTIMAL-20 (OPTIMAL minus 20) and OPTIMAL-40 (OPTIMAL minus 40). Let us now define achievement rate between the real value of the log-likelihood function and the local optimal solution as shown in the following:
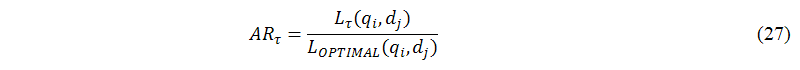
where Lτ(qi,dj) denotes the value of the log-likelihood function derived from different τs, where τ∈{SYSTEM, OPTIMAL, OPTIMAL-20, OPTIMAL-40}.
Table 8 shows all achievement rates over 10,000 simulation runs. For paper length limit, the number in each digit cell (except the first column and the last row) is the average value over 2,000 simulation runs. The average achievement rates for different τs are 1 (OPTIMAL), 0.998425 (OPTIMAL-20), 0.998162 (SYSTEM), and 0.638627 (OPTIMAL-40), respectively.
| Number of Runs | OPTIMAL | OPTIMAL-20 | SYSTEM | OPTIMAL-40 |
| 2000 | 1 | 0.998327 | 0.998132 | 0.642190 |
| 4000 | 1 | 0.998604 | 0.998397 | 0.636356 |
| 6000 | 1 | 0.998499 | 0.998174 | 0.636982 |
| 8000 | 1 | 0.998423 | 0.998086 | 0.639718 |
| 10000 | 1 | 0.998274 | 0.998023 | 0.637890 |
| Average | 1 | 0.998425 | 0.998162 | 0.638627 |
Table 9 shows the number of iterations required to run for different τs. The average number of iterations for different τs are 58.41875 (OPTIMAL), 38.41875 (OPTIMAL-20), 31.36200 (SYSTEM), and 18.41875 (OPTIMAL-40), respectively. The average number of iterations for OPTIMAL-20 and OPTIMAL-40 can be derived from OPTIMAL. In the case of SYSTEM, the number of iterations fluctuates since each run was dynamically terminated.
| Number of Runs | OPTIMAL | OPTIMAL-20 | SYSTEM | OPTIMAL-40 |
| 2000 | 58.28225 | 38.28225 | 31.19150 | 18.28225 |
| 4000 | 58.13029 | 38.13029 | 31.17996 | 18.13029 |
| 6000 | 58.28259 | 38.28259 | 31.27647 | 18.28259 |
| 8000 | 58.70122 | 38.70122 | 31.58823 | 18.70122 |
| 10000 | 58.69741 | 38.69741 | 31.57382 | 18.69741 |
| Average | 58.41875 | 38.41875 | 31.36200 | 18.41875 |
For any two cases, we define cost effective ratio between τ1 and τ2 by dividing the increased achievement rate by the increased percentage of the number of iterations as follows:
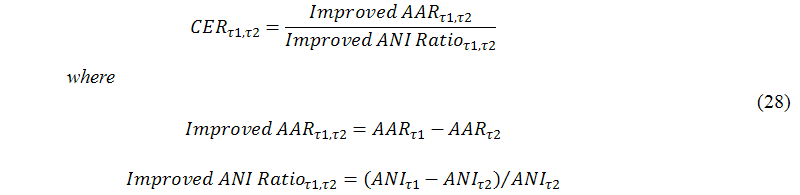
Using τ2=OPTIMAL-40 as a benchmark, the cost effective ratio values for different τs, SYSTEM, OPTIMAL-20, and OPTIMAL are shown in Table 10. We found that τ1=SYSTEM significantly outperforms other τs, and the cost effective ratio values drop rapidly beyond τ1=SYSTEM.
| OPTIMAL-40 | SYSTEM | OPTIMAL-20 | OPTIMAL | |
| Average Achievement Rate | 0.638627 | 0.998162 | 0.998425 | 1 |
| Average Number of Iterations | 18.41875 | 31.36200 | 38.41875 | 58.41875 |
| Improved Average Achievement Rate | 0.562981208 | 0.563393 | 0.565859 | |
| Improved Average Number of Iteration Ratio | 0.702721412 | 1.085850 | 2.171700 | |
| Cost Effective Ration | 0.801144236 | 0.518850 | 0.260561 |
In summary, we conclude that our method can yield a cost effective solution in a comparatively short amount of time.
In this paper, we presented an integrated keyword suggestion system that consists of two stages: training and suggestion. The training stage applies the latent semantic analysis and probabilistic latent semantic analysis methods to form the training parameter. Then, the suggestion stage applies a semantic graph to generate a list of suggested keywords. The suggested keywords generated from our system have a strong semantic relationship between the user's query and each suggested keyword.
This paper has three main contributions: first, we have presented a high-performance keyword suggestion system. According to the results of the simulation and user evaluation studies, our system was found to be better than other online systems. Secondly, we have shown that the value of the log-likelihood function obtained from our system is a cost effective solution in a comparatively short amount of time. Thirdly, we also have shown that the initial parameters obtained from the latent semantic analysis probability model are superior to the random probability model.
Currently, we used the latent semantic analysis probability model as the initial parameters since singular value decomposition may introduce negative values in the result of latent semantic analysis and such values cannot be treated as a probability distribution. In the future, we plan to use the non-negative matrix factorization model to deal with the problem of negative values in the process of singular value decomposition. On the other hand, the suggested keywords may be out-of-date since the training stage uses a batch processing to update the relevant parameters. We also plan to integrate the Web snippet analysis into our training stage to suggest up-to-date keywords.
This work was supported in part by National Science Council, Taiwan under grant NSC 97-2221-E-259-026.
Lin-Chih Chen is an assistant professor in the Department of Information Management at National Dong Hwa University, Taiwan. His research interests include Web intelligent and Web technology. He develops many Web intelligent systems include the Cayley search engine, the LIK keyword suggestion system, the Cayley digital content system, the iClubs community, language agents, and a Web snippet clustering system. He is also a leader of the Cayley group. He can be contacted at lcchen@mail.ndhu.edu.tw
| Find other papers on this subject | ||
© the author, 2010. Last updated: 28 February, 2010 |