vol. 14 no. 4, Decenber, 2009
vol. 14 no. 4, Decenber, 2009 | ||||
The point of departure of Larsen's criticism is that the application of the whole counting method constitutes a 'problem of non-additivity'. This problem applies to the attribution of papers to unique institutions in address fields in bibliographic records representing Swedish research published during the period 1998-2006. The objective of this research was to visualize the regional publications structure and to provide a regional research profile based on national baselines. The points of criticism in Larsen's paper are reviewed in the same order as they appear in his critique.
To begin with, Larsen is not satisfied with the reference to Gauffriau et al. (2007) and claims that it is 'not in agreement with the results described in this reference'. On page 177 in Gauffriau (2007) the authors state that:
There is a close consensus about three main counting methods, whole counting, fractional counting, and first author counting. In whole counting, all unique countries, institutions or authors contributing to a paper receive one credit. In fractional counting, one credit is shared between the unique countries, institutions or authors with equal fractions to each participant. (Gauffriau et al. 2007: 177)
My purpose with this reference was to confirm consensus about three basic counting methods in a current paper. As my study did not involve the comparison of different counting methods, I did not elaborate on this issue any further. Notably, nineteen counting methods are discussed by Gauffriau and colleagues.
Larsen claims that 'the object of study' and the 'basic unit of analysis' must be stated. I have no objections, though it would seem to be a superfluous comment as I state that 'the publication frequency of an institution was counted as the number of articles in which its standardized name occurred' (Jarneving 2009). Hence, both objects of study as well as analysed units are covered.
Citing my comments on fractional counting, 'fractional counting implies a difficulty as there is no clear correspondence between authors and corporate addresses', Larsen comments that this is correct but only relevant if author numbers are considered. It is not clear what Larsen's point is. Should author numbers be considered or not? Under the assumption that each author contributes more or less equally, the proportion of authors in a paper associated with a certain institution in the same paper should be reflected. Given the applied data source and period of observation, such associations cannot be discerned. Assume the bibliographic description of a paper containing three authors and two unique institutions:
The first author may be associated with the first institution (U1), however the associations between the two other authors (B and C) and corresponding institutions are not known, nor do we know if these authors are associated with more than one of the institutions. Assume we actually knew all the associations between these authors and their institutions. Then we may arrive at the following solution:
and we would assign one-third of a paper to U1 and two-thirds to U2.
Applying fractional counting without considering author numbers, we would assign half of a paper to each institution. Given the aforementioned assumption, this does not result in a fair distribution of the paper. Should we agree that author numbers are irrelevant we may dismiss the problem. However, in that case we need to present good arguments in favour of the dismissal.
In European Commission (2003), the counting method applied by Centre for Science and Technology Studies is presented:
[t]here is no fair method to determine how much money, effort, equipment and expertise each researcher, institute or country contribute[s] to a paper and the underlying research effort. Dividing up a paper between the participating units is therefore to some extent arbitrary. Our basic assumption is that each author, main institution and country listed in the affiliated addresses made a non-negligible contribution. Each paper is therefore assigned in the full to all unique authors, institutions and countries listed in the address heading.
This quotation reflects the problem from another angle. Basically, there is no fair way of dividing up a paper as we cannot measure factual research efforts by bibliometric methods. Clearly, bibliographic data do not mirror this variable exhaustively. Hence, one may assume that even if associations between authors and institutions were available, a fair dividing-up of papers would still not be possible. The solution of the Centre was to assign one full paper to every unique author, institution and country in the address field. Larsen comments that fractional counting has been used by OECD since 2001. This is a statement of fact, not an argument.
In Glänzel (1996) under '2. Proposals for standardisation based on experiences made at ISSRU, the author claims,whilst at the macro-level all three methods may yield satisfactory results, at lower levels of aggregation first-address counts proved to be inappropriate and especially at the micro-level whole counts should be preferred to fractional counts.
Larsen suggests that my citation is 'distorted', but to me it appears that the appropriateness of the whole counting method on lower levels of aggregation, especially at the micro-level, but not exclusively, is indicated. However, this may be a matter of interpretation.
Larsen highlights that results from whole counting are not additative. This means that the sum of papers assigned to analysed units does not equal the total number of unique papers applied in the analysis. Duplicate counting also occurs when counting papers assigned to more than one subject category. 'The value' for the region, mentioned by Larsen, may aim at the total contribution of the region within a field or the total sum of contributions in all fields. In either instance, this value may be represented by (1) fractional counts, (2) whole counts or (3) first author counts of papers. Hence, 'the value' may reflect different parameters. The choice of counting method concerns what aspects one wants to map and the underlying assumptions. For instance, if first author counts were applied, we would assume that the position of the first author (institution) in the majority of cases indicates the major contributor and focus our inferring of results on this particular aspect. Fractional counting mirrors the influence of co-authorship whereas whole counting depicts the volume of papers associated with a particular source. Though fractional counting is more satisfying from a mathematical point of view, this alone does not motivate a general preference of the method. Larsen does not inform the reader if he actually considers fractional counting the generally preferred counting method. However, it seems implicitly stated.
Larsen's reference to Anderson et al. (1988) seems to concern problems when the European Union is compared with USA, using the whole counting method (Gauffriau et al. 2007). In my paper, countries and regions are not compared and the two research settings are hardly comparable.
Conclusively, fractional counting does not provide a 'fair' dividing up of a paper as associations between authors are not considered. In this sense, neither would the whole counting method. The origin of the problem is the lack of information that measures contributions. This means that there is no generally preferred method of counting and the choice of method would depend on the characteristics of the features that require mapping. Ultimately, you could reflect the influence of institutions from more than one perspective.
Larsen also criticizes the combination of the whole counting method with the activity index, which was presented in Schubert and Braun (1986) as the country's share in world's publication output in the given field over the country's share in world's publication output in all science fields, and adjusted to the regional (sub-national level) so that 'the numerator is the region's share in the nation's publication output in the given field and the denominator the region's share in the nation's total output in all science fields' (Jarneving, 2009).
This index provides an approximation of the relative research effort devoted to a regional field in relation to a national baseline. In a balanced situation, the proportion of regional papers in a national field is the same as the proportion of regional papers in the national total. The index measures the internal balance within the region with regard to publication activity within fields, hence the name.
With regard to the whole counting method, Larsen's claims that 'Only if the region studied has exactly the same extent of cooperation with scientists outside the region in all fields will values be meaningful'. I would say this is a matter of how to measure activity, which is problematic as previously established. Applying the whole counting method, less collaborative fields and highly collaborative fields are treated in the same way. According to Larsen, this leads to meaningless information as the influence of extra-regional collaboration is not taken into account. However, this is a type of circular argument that leads nowhere. In Gauffrie et al. (2007), it is stated 'if there was no cooperation, all counting methods would produce the same result', hence, the choice of counting methods is related to the issue of collaboration. In this particular case, the choice of method would depend on whether one wants to mirror the influence of domestic (non-regional) and foreign institutions, or count the frequency of regional participation in national paper production. If satisfied with the definition of the national total as the set of papers with at least one Swedish address, we would not discriminate between domestic and foreign contributions when counting shares. If not satisfied with this definition, we may redefine the national total so that it corresponds to the total of domestic fractions. Hence, fractional counting is problematic with regard to the notion of a national total.With reference to Price's elaborations on doubling periods of science indicators in the USA and Europe (1961), Larsen finds the linear growth of the regional and Swedish article production surprising, as an exponential growth rate should be expected. With regard to the data accounted for in my paper, a linear function provides a better correspondence. Should we augment the observation period it is possible to relate an exponential function to data. In Figure 1 publication data from Web of Science, Science Citation Index Expanded and Scopus, Life Sciences, Health Sciences and Physical Sciences for the period 1975 to 2006 are applied to mirror the growth of Swedish research. As can be seen, the interval corresponding to the observation period is linear for both curves.
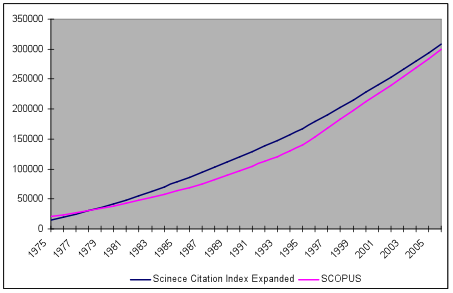
With reference to Figure 1 in the empirical study, Larsen observes that there is a slight increase in the regional share of the national total and suggests that this may be caused only by increased cooperation with other regions and countries. With regard to the applied counting method, one can only make the claim that the increase of papers over time reflects an increasing share of papers with at least one regional author. Hence, the volume of articles associated with regional research was mirrored. Larsen argues that, 'it will be possible for all institutions to increase their shares over time by increasing cooperation, even if the total output of papers is constant'. This is true, but the other side of the coin is that fractional counting would not map the regional paper production, and both aspects may be of interest. However, these issues hardly constitute a problem and it is rather a question of what aspects one chooses to map, i.e., what is considered useful information in a certain context.
Finally, Larsen gets back to the 'problem' of non-additivity referring to Table 1, addressing the problem with respect to the rank ordering of institutions. Larsen argues that this problem clearly shows up in the case of Physics as the total of 114 % is reached when adding the percentages. In the first place, adding up the percentages is a meaningless operation in this context, and I maintain that the purpose of this table is in agreement with the applied counting method as the objective was to map the institutional influence in terms of percentage coverage (Jarneving 2009).
Summing up, although interesting, Larsen's criticism is unfocused as he applies a circular argument where non-additivity is presumed, but not proved, to be a problem other than in a mathematical sense. Larsen fails to demonstrate how fractional counting would produce valid results, while the whole counting method would not. We may conclude that no generally preferred method exists and this is reflected in the existence of several methods of counting. In this particular case, fractional counting would have provided complementary information, but could not substitute for the whole counting method.
| Find other papers on this subject | ||
© the author, 2009. Last updated: 5 November, 2009 |